PICASSO
High Performance R and Python Library for Sparse Learning
PICASSO (PathwIse CalibrAted Sparse Shooting algOrithm) implements a unified framework of pathwise coordinate optimization for a variety of sparse learning problems (e.g., sparse linear regression, sparse logistic regression, sparse Poisson regression and scaled sparse linear regression) combined with efficient active set selection strategies. The core algorithm is implemented in C++ with Eigen3 support for portable high performance linear algebra. Runtime profiling is documented in the Performance section.
Table of contents
- Directory structure
- Introduction
- Background
- The Power of Nonconvex Penalties
- Performance
- Installation
- Tutorials
- References
Directory structure
The directory is organized as follows:
-
src: C++ implementation of the PICASSO algorithm.
- c_api: C API as an interface for R and Python package.
- objective: Objective functions, which includes linear regression, logsitic regression, poisson regression and scaled linear regression.
- solver: Two types of pathwise active set algorithms. Actgd.cpp implements pathwise active set + gradient descent. Actnewton.cpp implements pathwise active set + newton algorithm.
- include
- amalgamation:flag all the c++ implementation for compiling.
- cmake:Makefile local configurations.
- make:Makefile local configurations.
- R-package: R wrapper for the source code.
- python-package: Python wrapper for the source code.
- tutorials: tutorials for using the code in R and Python.
- profiling: profiling the performance from R package.
Introduction
The pathwise coordinate optimization is undoubtedly one the of the most popular solvers for a large variety of sparse learning problems. By leveraging the solution sparsity through a simple but elegant algorithmic structure, it significantly boosts the computational performance in practice (Friedman et al., 2007). Some recent progresses in (Zhao et al., 2017; Li et al., 2017) establish theoretical guarantees to further justify its computational and statistical superiority for both convex and nonvoncex sparse learning, which makes it even more attractive to practitioners.
We recently developed a new library named PICASSO, which implements a unified toolkit of pathwise coordinate optimization for solving a large class of convex and nonconvex regularized sparse learning problems. Efficient active set selection strategies are provided to guarantee superior statistical and computational preference.
The pathwise coordinate optimization framework with 3 nested loops : (1) Warm start initialization; (2) Active set selection, and strong rule for coordinate preselection; (3) Active coordinate minimization. Please refer to tutorials/PICASSO.pdf for details of the algorithm design.
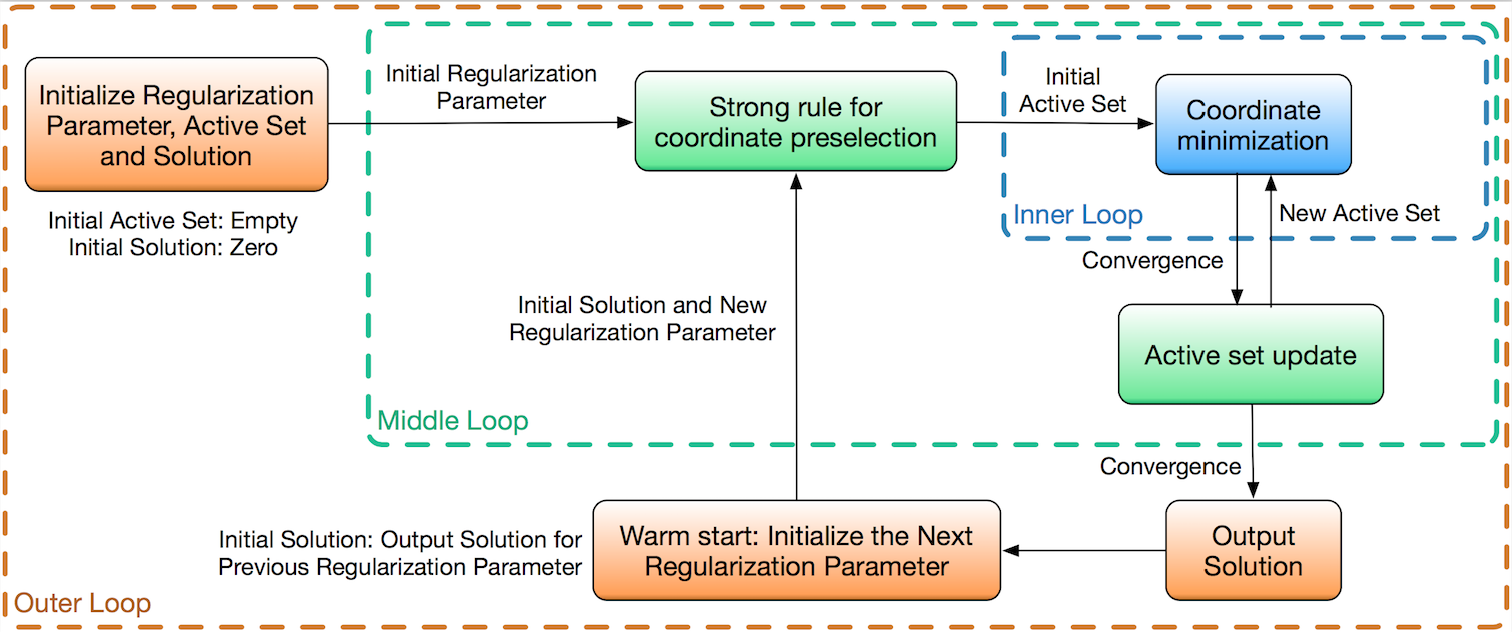
Background
There exists several R pakcages (such as ncvreg and glmnet) which implement state-of-the-art heuristic optimization algorithms for sparse learning. However they either lack support for nonconvex penalties or becomes very unstable when there are multi-colinear features. PICASSO combines pathwise coordinate optimization and multi-stage convex relaxation for nonconvex optimization and finds a ‘good’ local minimal which has provable statistical property.
Power of Nonconvex Penalties
L1 penalized regression (LASSO) is a useful tool for feature selection but it tends to give very biased estimator due to the penalty term. As demonstrated in the example below, the lowest estimation error among all the lambdas computed is as high as 16.41%.
> set.seed(2016)
> library(glmnet)
> n <- 1000; p <- 1000; c <- 0.1
> # n sample number, p dimension, c correlation parameter
> X <- scale(matrix(rnorm(n*p),n,p)+c*rnorm(n))/sqrt(n-1)*sqrt(n) # n is smaple number,
> s <- 20 # sparsity level
> true_beta <- c(runif(s), rep(0, p-s))
> Y <- X%*%true_beta + rnorm(n)
> fitg<-glmnet(X,Y,family="gaussian")
> # the minimal estimation error |\hat{beta}-beta| / |beta|
> min(apply(abs(fitg$beta - true_beta), MARGIN=2, FUN=sum))/sum(abs(true_beta))
[1] 0.1641195
Nonconvex penalties such as SCAD [1] and MCP [2] are statistically better but computationally harder. The solution for SCAD/MCP penalized linear model has much less estimation error than lasso but calculating the estimator involves non-convex optimization. With limited computation resource, we can only get a local optimum which probably lacks the good property of the global optimum.
The PICASSO package [3, 4] solves non-convex optimization through multi-stage convex relaxation. Although we only find a local minimum, it can be proved that this local minimum does not lose the superior statistcal property of the global minimum. Multi-stage convex relaxation is also much more stable than other packages (see benchmark below).
Let’s see PICASSO in action — the estimation error drops to 6.06% using SCAD penalty from 16.41% error produced by LASSO.
> library(picasso)
> fitp <- picasso(X, Y, family="gaussian", method="scad")
> min(apply(abs(fitp$beta-true_beta), MARGIN=2, FUN=sum))/sum(abs(true_beta))
[1] 0.06064173
Performance
$cd profiling
$Rscript benchmark.R
$python benchmark.py
R package
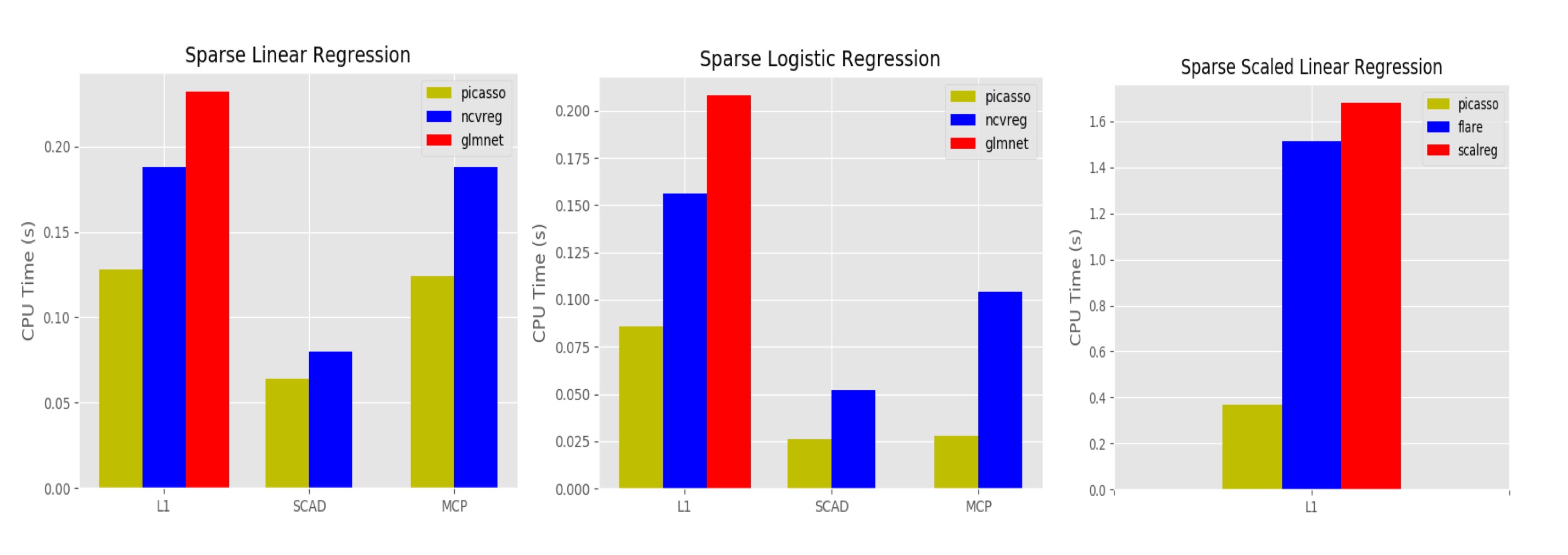
- Sparse linear regression. picasso achieves similar timing and optimization performance to glmnet and ncvreg.
- Sparse logistic regression. When using the l1 regularizer, picasso, glmnet and ncvreg achieves similar optimization performance. When using the nonconvex regularizers, picasso achieves significantly better optimization performance than ncvreg, especially in ill-conditioned cases.
- Scaled sparse linear regression. Picasso significantly outperforms scalreg and flare in timing performance. In Table 5.3 in tutorials/PICASSO.pdf, picasso is 20 − 100 times faster and achieves smaller objective function values.
Details of our benmarking process are documented in tutorials/PICASSO.pdf.
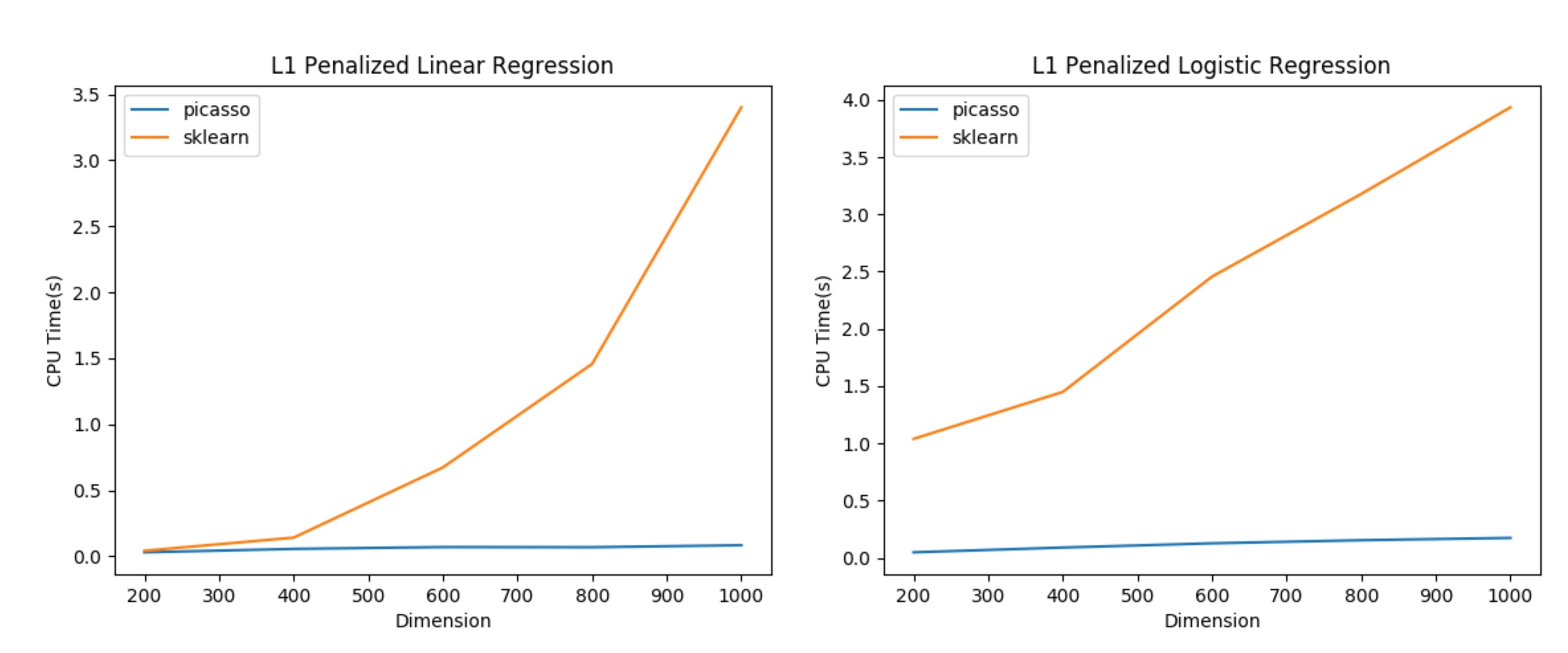
Python package
We compared with sklearn (version 0.19.1) for L1 regularized linear and logistic regression. For linear regression, we compare against sklearn.linear_model.lasso_path and for logistic regression, we compare against sklearn.linear_model.LogisticRegression (with liblinear backend). Details of the experiments can be found in the script profiling/benchmark.py. Fixing sample number as 500 and we change sample dimension, PICASSO’s run time also most does not depend on dimension thanks to the active set strategy. Precision parameters of the optimization are adjusted so that equal objective function values are achieved.
Installation
Installing R package
There are two ways to install the picasso R package.
- Installing from CRAN (recommended). The R package is hosted on CRAN. The easiest way to install R package is by running the following command in R
install.packages("picasso") - Installing from source code.
$ git clone https://github.com/jasonge27/picasso.git $ cd picasso; make Rinstall
Installing Python package
There are two ways to install the picasso python package.
- Installing from PyPi (recommended).
pip install pycasso --user. - Installing from source code.
$git clone https://github.com/jasonge27/picasso.git $cd picasso; make Pyinstall
You can test if the package has been successfully installed by python -c "import pycasso; pycasso.test()
Details for installing python package can also be found in document or github
Tutorials
Check the R tutorial in tutorials/tutorial.R and Python tutorial in tutorials/tutorial.py. Let us know if anything is hard to use or if you want any other features.
References
[1] Jianqing Fan and Runze Li, Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties, 2001
[2] Cun-Hui Zhang, Nearly Unbiased Variable Selection Under Minimax Concave Penalty, 2010
[3] Xingguo Li, Jason Ge, Haoming Jiang, Mingyi Hong, Mengdi Wang, and Tuo Zhao, Boosting Pathwise Coordinate Optimization in High Dimensions: Sequential Screening and Proximal Sub-sampled Newton Algorithm, 2016
[4] Tuo Zhao, Han Liu, and Tong Zhang, Pathwise Coordinate Optimization for Nonconvex Sparse Learning: Algorithm and Theory, 2014
[5] Xingguo Li,Lin F. Yang, Jason Ge, Jarvis Haupt, Tong Zhang and Tuo Zhao, On Quadratic Convergence of DC Proximal Newton Algorithm in Nonconvex Sparse Learning, 2017